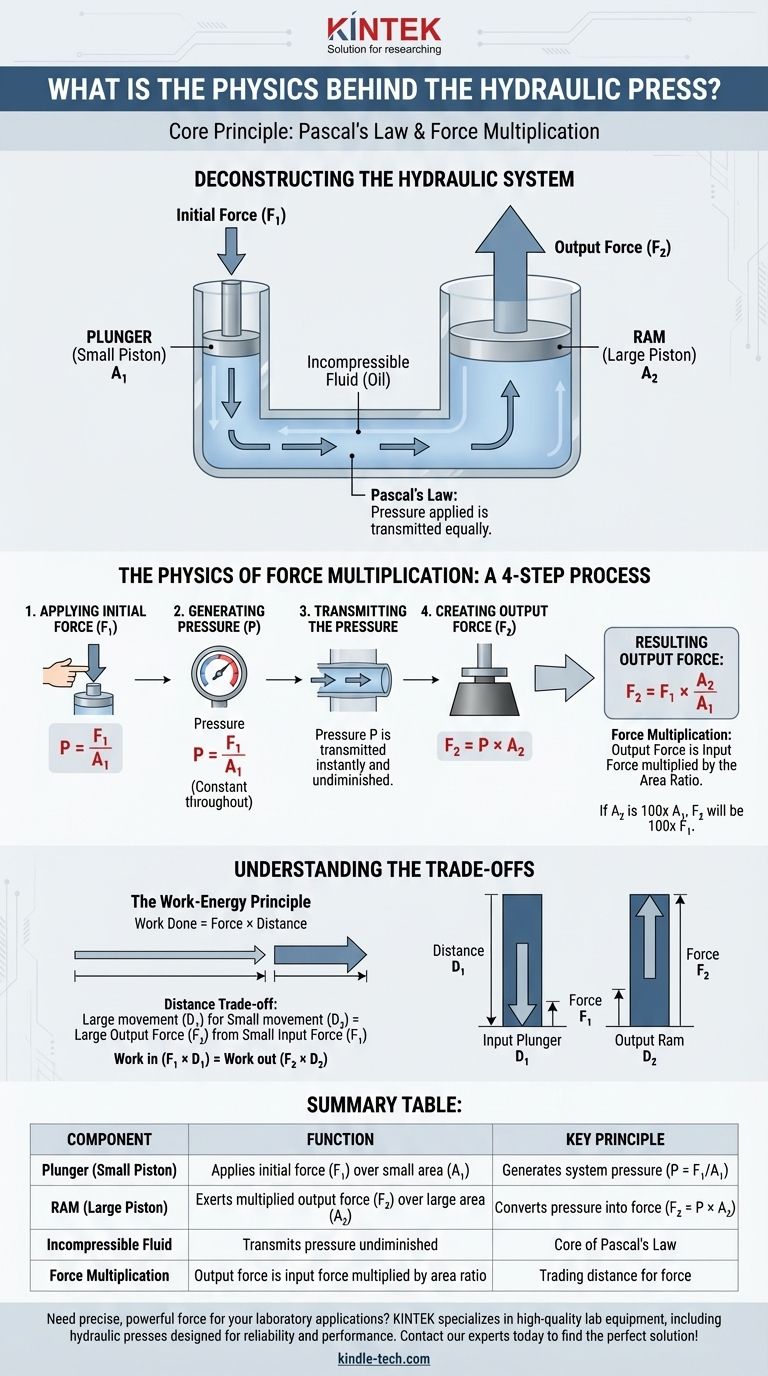
Il principio fondamentale alla base di una pressa idraulica è la Legge di Pascal, che consente un'immensa moltiplicazione della forza utilizzando un fluido incomprimibile. Questa legge afferma che qualsiasi pressione applicata a un fluido all'interno di un sistema chiuso viene trasmessa in modo uguale in tutto il fluido. Una pressa idraulica sfrutta questo principio utilizzando una piccola forza iniziale su una piccola area per generare una forza di uscita molto maggiore su un'area più ampia.
L'intuizione fondamentale è che una pressa idraulica non crea energia, ma moltiplica la forza. Lo fa convertendo una piccola forza applicata su un piccolo pistone in una pressione a livello di sistema, che poi agisce su un pistone più grande per produrre una forza di uscita proporzionalmente maggiore.
Scomporre il Sistema Idraulico
Per comprendere la fisica, dobbiamo prima esaminare i componenti essenziali che costituiscono qualsiasi pressa idraulica. Queste parti lavorano insieme in un sistema chiuso per trasferire e moltiplicare la forza.
I Due Pistoni: Stantuffo e Cilindro di Spinta
Quasi ogni pressa idraulica ha due pistoni di dimensioni diverse. Il pistone più piccolo, spesso chiamato stantuffo (plunger), è dove viene applicata la forza iniziale, più piccola. Il pistone più grande, noto come cilindro di spinta (ram), è quello che esercita la massiccia forza di compressione per eseguire il lavoro.
Il Fluido Incomprimibile
I pistoni sono alloggiati in cilindri collegati da un canale riempito di un fluido incomprimibile, tipicamente un olio speciale. "Incomprimibile" è la proprietà chiave: significa che il volume del fluido non cambia sotto pressione. Ciò assicura che quando si spinge il fluido da un'estremità, questo trasmette immediatamente quella forza all'altra estremità senza essere "schiacciato".
La Fisica della Moltiplicazione della Forza
Il vero genio della pressa idraulica risiede nel modo in cui utilizza la relazione tra forza, pressione e area. Il processo è una chiara applicazione in quattro fasi della Legge di Pascal.
Fase 1: Applicazione della Forza Iniziale (F₁)
Il processo inizia quando una forza relativamente piccola (F₁) viene applicata al piccolo pistone di ingresso, lo stantuffo. Questo pistone ha una piccola area superficiale (A₁).
Fase 2: Generazione della Pressione (P)
Questa forza iniziale genera pressione all'interno del fluido idraulico. L'entità della pressione è definita dalla formula Pressione = Forza / Area. Quindi, la pressione (P) nel sistema è calcolata come P = F₁ / A₁.
Fase 3: Trasmissione della Pressione
Qui è dove la Legge di Pascal è fondamentale. La legge garantisce che la pressione (P) che hai appena creato venga trasmessa istantaneamente e senza attenuazione a ogni parte del fluido racchiuso. La pressione che agisce sul grande cilindro di spinta è esattamente la stessa della pressione sotto il piccolo stantuffo.
Fase 4: Creazione della Forza di Uscita (F₂)
Questa pressione costante (P) spinge ora contro il grande pistone di uscita, il cilindro di spinta, che ha un'area superficiale molto più grande (A₂). La forza di uscita risultante (F₂) è calcolata riorganizzando la formula della pressione: Forza = Pressione × Area.
Pertanto, la forza di uscita è F₂ = P × A₂.
Poiché sappiamo che P = F₁ / A₁, possiamo sostituirla nella seconda equazione per vedere la relazione diretta: F₂ = (F₁ / A₁) × A₂. Questo può essere semplificato per mostrare che la forza di uscita è la forza di ingresso moltiplicata per il rapporto delle aree: F₂ = F₁ × (A₂ / A₁).
Se l'area del cilindro di spinta (A₂) è 100 volte maggiore dell'area dello stantuffo (A₁), la forza di uscita (F₂) sarà 100 volte maggiore della forza di ingresso (F₁).
Comprendere i Compromessi
Questa moltiplicazione della forza non viola le leggi della fisica e non è una fonte di energia gratuita. Esiste un compromesso fondamentale dettato dalla conservazione dell'energia.
Il Principio Lavoro-Energia
In un sistema ideale, il lavoro compiuto sul pistone di ingresso deve essere uguale al lavoro compiuto dal pistone di uscita. Il lavoro è calcolato come Lavoro = Forza × Distanza.
Il Compromesso sulla Distanza
Poiché la forza di uscita (F₂) è molto maggiore della forza di ingresso (F₁), la distanza percorsa dal cilindro di spinta di uscita (D₂) deve essere proporzionalmente minore della distanza percorsa dallo stantuffo di ingresso (D₁).
Per sollevare il massiccio cilindro di spinta di un solo pollice, potrebbe essere necessario spingere lo stantuffo piccolo verso il basso di 100 pollici. Si sta scambiando un lungo movimento con una bassa forza per un breve movimento con un'alta forza.
Fare la Scelta Giusta per il Tuo Obiettivo
Comprendere questo principio ti permette di applicarlo a diversi obiettivi, sia nella progettazione, nel funzionamento o nella semplice comprensione.
- Se il tuo obiettivo principale è la progettazione: Concentrati sul rapporto tra le aree dei pistoni (A₂/A₁), poiché questo rapporto determina direttamente il fattore di moltiplicazione della forza del tuo sistema.
- Se il tuo obiettivo principale è il funzionamento: Riconosci che, sebbene la forza generata sia immensa, il movimento del cilindro di spinta sarà lento e deliberato. Questo compromesso forza-distanza è una caratteristica operativa e di sicurezza fondamentale.
- Se il tuo obiettivo principale è la comprensione: Il punto chiave è che la pressione rimane costante in un fluido chiuso, consentendo a una piccola forza su una piccola area di diventare una grande forza su una grande area.
Padroneggiando questo principio, puoi vedere come la semplice meccanica dei fluidi abilita alcuni dei macchinari più potenti del mondo moderno.
Tabella Riassuntiva:
| Componente | Funzione | Principio Chiave |
|---|---|---|
| Stantuffo (Pistone Piccolo) | Applica la forza iniziale (F₁) su una piccola area (A₁) | Genera pressione di sistema (P = F₁/A₁) |
| Cilindro di Spinta (Pistone Grande) | Esercita la forza di uscita moltiplicata (F₂) su una grande area (A₂) | Converte la pressione in forza (F₂ = P × A₂) |
| Fluido Incomprimibile | Trasmette la pressione senza attenuazione attraverso il sistema | Nucleo della Legge di Pascal |
| Moltiplicazione della Forza | La forza di uscita è la forza di ingresso moltiplicata per il rapporto delle aree (F₂ = F₁ × (A₂/A₁)) | Ottenuta scambiando distanza con forza |
Hai bisogno di una forza precisa e potente per le tue applicazioni di laboratorio? KINTEK è specializzata in attrezzature da laboratorio di alta qualità, comprese presse idrauliche progettate per affidabilità e prestazioni esatte. Sia che tu stia comprimendo campioni, modellando materiali o necessiti di un'applicazione di forza personalizzata, la nostra esperienza ti assicura di ottenere lo strumento giusto per le tue esigenze. Contatta oggi i nostri esperti per trovare la soluzione di pressa idraulica perfetta per il tuo laboratorio!
Guida Visiva
Prodotti correlati
- Fornace a Pressa Calda a Induzione Sottovuoto 600T per Trattamento Termico e Sinterizzazione
- Fornace Sottovuoto a Pressa Calda Macchina a Pressa Sottovuoto Fornace Tubolare
- Fornace a Tubo Sottovuoto per Laboratorio ad Alta Pressione
- Fornace per Trattamento Termico Sottovuoto e Sinterizzazione con Pressione d'Aria di 9 MPa
- Fornace a Tubo di Quarzo da Laboratorio da 1400℃ con Forno Tubolare in Tubo di Allumina
Domande frequenti
- Quali prodotti sono realizzati mediante pressatura a caldo? Ottieni la massima densità e prestazioni per i tuoi componenti
- Perché le giunzioni brasate sono soggette a cedimenti per fatica? Comprendere i fattori critici per giunzioni durature
- La brasatura o la saldatura è più economica? Un'analisi dettagliata dei costi per il tuo progetto
- Da cosa dipende la forza del legame nella saldobrasatura? Padroneggia le 3 chiavi per un giunto forte
- Qual è l'effetto dell'aumento della pressione durante la sinterizzazione? Raggiungere la massima densità e prestazioni superiori
