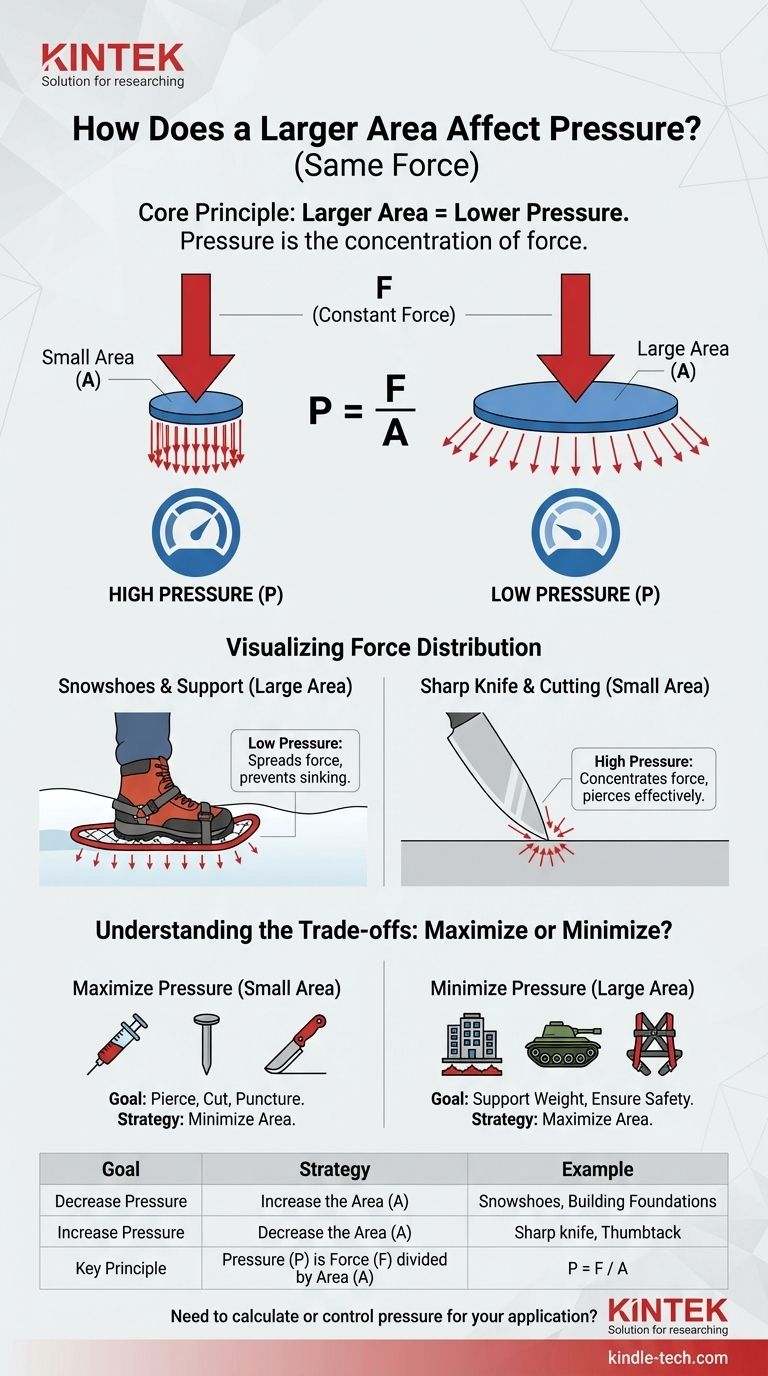
In breve, un'area più grande diminuisce la pressione esercitata dalla stessa forza. La relazione è inversamente proporzionale: all'aumentare dell'area su cui viene applicata una forza costante, la pressione in qualsiasi punto di quella superficie diminuisce. Questo perché la stessa quantità di forza viene distribuita su una superficie più ampia.
Il principio fondamentale da comprendere è che la pressione non è la forza stessa, ma la concentrazione della forza. Aumentando l'area di contatto, si sta effettivamente diluendo la forza, portando a una riduzione della pressione.
La relazione fondamentale: pressione, forza e area
Per comprendere veramente questo concetto, dobbiamo esaminare la fisica semplice ma potente che lo sottende. L'interazione tra questi tre elementi governa tutto, da come un coltello taglia a come un edificio sta in piedi.
L'equazione fondamentale
La relazione è definita dall'equazione P = F / A.
- P sta per Pressione, che è la quantità di forza esercitata per unità di area.
- F sta per Forza, che è la spinta o la trazione su un oggetto (come il peso).
- A sta per Area, che è la superficie su cui la forza è distribuita.
Questa formula chiarisce che se la Forza (F) rimane costante, aumentare l'Area (A) al denominatore causerà inevitabilmente una diminuzione della Pressione (P) risultante.
Un'analogia intuitiva: un letto di chiodi
Immagina di provare a stare in piedi su un singolo chiodo. L'intero peso del tuo corpo (la forza) sarebbe concentrato sulla minuscola punta di quel chiodo, creando un'immensa pressione che perforerebbe facilmente il tuo piede.
Ora, immagina un letto di migliaia di chiodi. Quando ti sdrai, il tuo stesso peso corporeo è ora distribuito uniformemente sulle punte di tutti quei chiodi. L'area totale è enorme, quindi la pressione di ogni singolo chiodo è incredibilmente piccola e non sufficiente a rompere la pelle. La forza non è cambiata, ma l'area sì, cambiando radicalmente il risultato.
Visualizzazione della distribuzione della forza
Pensa alla forza come a una quantità fissa di acqua e all'area come al contenitore in cui la versi.
Se versi l'acqua in un bicchiere alto e sottile (una piccola area), il livello dell'acqua sarà alto (alta pressione). Se versi la stessa quantità di acqua in una padella larga e poco profonda (una grande area), il livello dell'acqua sarà molto basso (bassa pressione). La quantità di acqua non è mai cambiata, solo la sua concentrazione.
Esempi pratici nella vita di tutti i giorni
Questo principio non è solo teorico; è un aspetto fondamentale dell'ingegneria e del design con cui interagisci costantemente.
Perché le racchette da neve funzionano
Il peso di una persona (forza) è costante. Quando si indossa uno stivale normale, quella forza è concentrata sulla piccola area della suola, facendoti affondare nella neve. Le racchette da neve aumentano drasticamente la superficie, distribuendo il tuo peso e abbassando la pressione ben al di sotto di quanto la neve possa sopportare.
L'affilatura di un coltello
Un coltello affilato ha una superficie estremamente piccola sul suo bordo tagliente. Questo design concentra la forza che applichi, creando un'immensa pressione che può facilmente tagliare i materiali. Un coltello smussato ha un'area più grande e arrotondata, che distribuisce la forza e richiede molto più sforzo per ottenere la stessa pressione di taglio.
Fondamenta degli edifici
I grattacieli sono incredibilmente pesanti. Per evitare che affondino nel terreno, vengono costruiti su fondamenta in cemento larghe e massicce. Queste fondamenta distribuiscono l'immenso peso (forza) dell'edificio su un'area molto ampia, assicurando che la pressione esercitata sul terreno sia sufficientemente bassa da essere supportata in sicurezza.
Puntine e aghi
Una puntina da disegno è un esempio perfetto di manipolazione di questo principio. Ha una testa grande e piatta per il pollice (grande area, bassa pressione per il comfort) e una punta affilata e minuscola per il muro (piccola area, alta pressione per una facile perforazione).
Comprendere i compromessi
L'obiettivo non è sempre quello di diminuire la pressione. Il design ottimale dipende interamente dalla funzione prevista e gli ingegneri devono scegliere se concentrare o distribuire la forza.
Quando l'alta pressione è l'obiettivo
In molte applicazioni, l'obiettivo è massimizzare la pressione. Ciò si ottiene minimizzando l'area di contatto per concentrare la forza applicata.
Esempi includono aghi da iniezione, chiodi, utensili da taglio e pattini da ghiaccio. L'intero scopo di questi progetti è creare una pressione sufficientemente alta da perforare una superficie con una forza minima.
Quando la bassa pressione è fondamentale
Al contrario, minimizzare la pressione è spesso una questione di sicurezza, stabilità o conservazione. Ciò si ottiene massimizzando l'area di contatto.
Esempi includono i larghi battistrada di un carro armato o di un bulldozer, le ampie cinghie di uno zaino pesante e le imbracature di sicurezza che distribuiscono la forza di una caduta su tutto il busto.
Fare la scelta giusta per il tuo obiettivo
Comprendere come manipolare la relazione tra forza, pressione e area è fondamentale per risolvere innumerevoli sfide fisiche.
- Se il tuo obiettivo principale è perforare, tagliare o bucare: devi concentrare la tua forza rendendo l'area di contatto il più piccola possibile.
- Se il tuo obiettivo principale è sostenere il peso o prevenire l'affondamento: devi distribuire la tua forza rendendo l'area di contatto il più grande possibile.
- Se il tuo obiettivo principale è garantire la sicurezza durante un impatto: devi dissipare la forza sull'area più ampia possibile per minimizzare la pressione su un singolo punto.
Dominare questo singolo principio ti consente di progettare e costruire strumenti più efficaci e strutture più sicure.
Tabella riassuntiva:
| Obiettivo | Strategia | Esempio |
|---|---|---|
| Diminuire la pressione | Aumentare l'area (A) | Racchette da neve, fondamenta di edifici |
| Aumentare la pressione | Diminuire l'area (A) | Coltello affilato, puntina da disegno, lama di pattino da ghiaccio |
| Principio chiave | La pressione (P) è la forza (F) divisa per l'area (A) | P = F / A |
Hai bisogno di calcolare o controllare la pressione per la tua applicazione? KINTEK è specializzata in attrezzature e materiali di consumo da laboratorio, fornendo gli strumenti e le competenze per aiutarti ad applicare questi principi fondamentali nella tua ricerca o nei processi di controllo qualità. Che tu stia progettando un nuovo prodotto o ottimizzando una procedura, il nostro team può aiutarti a selezionare l'attrezzatura giusta per misurare e gestire con precisione forza e pressione.
Contatta i nostri esperti oggi stesso per discutere le tue esigenze specifiche!
Guida Visiva
Prodotti correlati
- Macchina comprimitrice per compresse singola e macchina comprimitrice rotativa per la produzione di massa per TDP
- Macchina elettrica per la compressione di compresse a punzonatura singola TDP
- Macchina per compresse elettrica a punzone singolo Laboratorio pressa per compresse TDP
- Macchina per compresse rotativa a pugno singolo su scala di laboratorio Macchina per punzonatura di compresse TDP
- Anello per stampo per comprimitrice rotativa multi-punzone per stampi ovali e quadrati rotanti
Domande frequenti
- Quali sono gli svantaggi della lavorazione a pressa? Costi elevati e limiti di progettazione per la produzione di massa
- Quale tipo di pressa per compresse è più adatta per la produzione su larga scala? Presse rotative per un'efficienza ad alto volume
- Quali sono i vantaggi di una comprimitrice rotativa? Sblocca la produzione di compresse ad alta velocità e precisione
- Qual è la differenza tra una pressa per compresse a punzone singolo e una rotativa? Scegli la macchina giusta per il tuo laboratorio o la tua produzione
- Quanto è veloce la comprimitrice rotativa? Sblocca le massime velocità di produzione per le tue compresse
