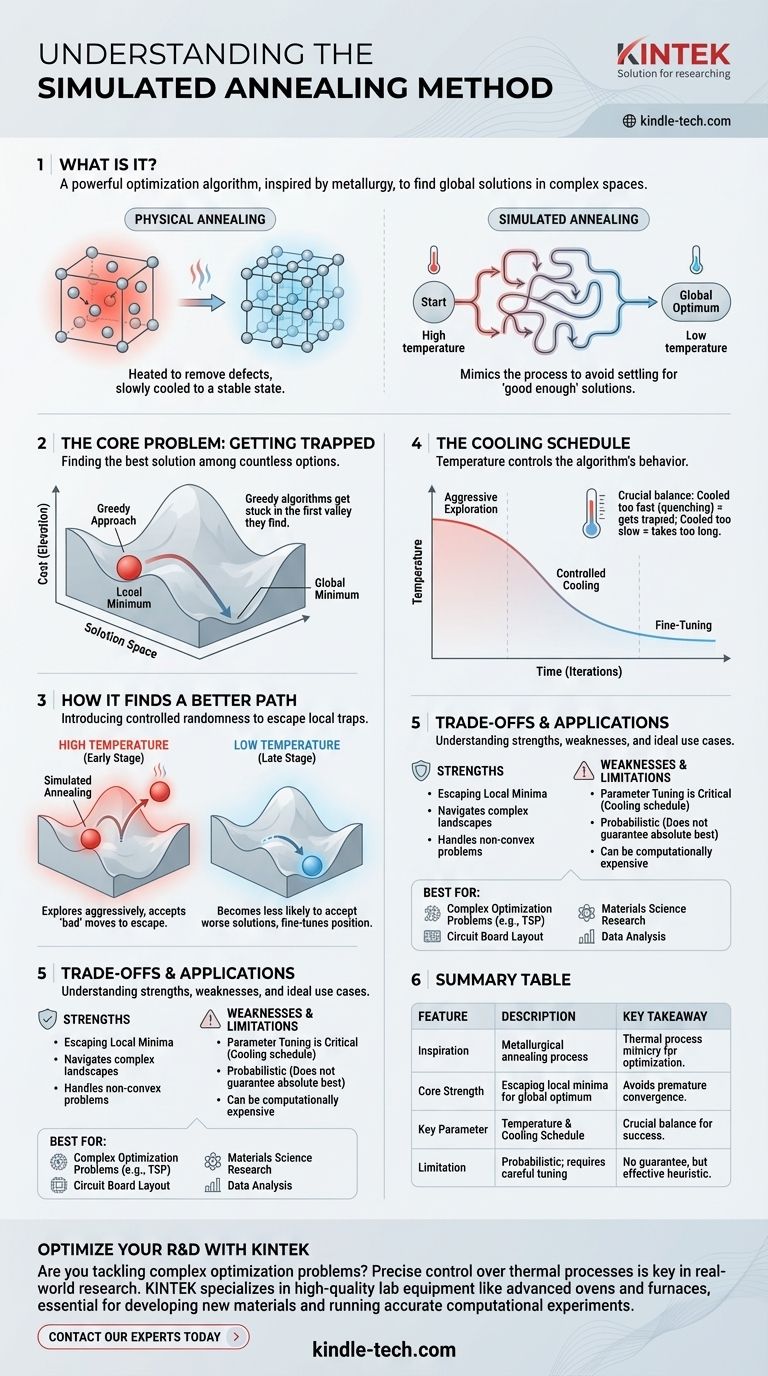
In breve, la ricottura simulata è un potente algoritmo di ottimizzazione utilizzato per trovare una buona (e spesso globale) soluzione in uno spazio di ricerca vasto e complesso. È direttamente ispirato al processo metallurgico di ricottura, in cui un materiale viene riscaldato e poi raffreddato lentamente per rimuovere difetti e raggiungere uno stato cristallino stabile a bassa energia. L'algoritmo imita questo processo fisico per risolvere problemi computazionali astratti.
Nella sua essenza, la ricottura simulata evita la trappola comune di accontentarsi di una soluzione "abbastanza buona" imitando il processo fisico di ricottura del metallo. Inizia esplorando un'ampia gamma di possibilità (alta temperatura) e gradualmente restringe il suo focus a una soluzione stabile e di alta qualità (bassa temperatura).
Il problema centrale: rimanere intrappolati
Per comprendere la ricottura simulata, devi prima capire il problema che risolve: trovare la migliore soluzione possibile tra innumerevoli opzioni, un compito noto come ottimizzazione.
Il panorama delle soluzioni
Immagina che ogni possibile soluzione al tuo problema sia un punto su un vasto paesaggio collinare. L'elevazione di ogni punto rappresenta il suo "costo": più bassa è l'elevazione, migliore è la soluzione. Il tuo obiettivo è trovare il punto più basso sull'intera mappa, il minimo globale.
L'approccio "greedy" e il suo difetto
Un algoritmo semplice, spesso chiamato hill-climbing (scalata della collina), partirebbe da un punto casuale e si muoverebbe sempre in discesa. Questo è un approccio "greedy" (avido) perché accetta solo mosse che producono un miglioramento immediato.
Il problema è che questo metodo rimarrà bloccato nella prima valle che trova — un minimo locale. Non ha modo di sapere se una valle molto più profonda, il minimo globale, esiste appena oltre la prossima collina.
Come la ricottura simulata trova un percorso migliore
La ricottura simulata supera questa limitazione introducendo un elemento controllato di casualità che le consente di sfuggire a queste trappole locali.
L'ispirazione: la ricottura fisica
In metallurgia, riscaldare un metallo conferisce ai suoi atomi energia sufficiente per muoversi liberamente, rompendo strutture subottimali e difettose. Man mano che il metallo viene raffreddato lentamente, gli atomi hanno il tempo di stabilirsi in un reticolo cristallino altamente ordinato e resistente, uno stato di minima energia.
L'algoritmo: la temperatura come manopola di controllo
La ricottura simulata adotta questo concetto introducendo un parametro di temperatura. Questa non è una temperatura fisica, ma una variabile che controlla il comportamento dell'algoritmo.
L'algoritmo inizia con una temperatura elevata. In questo stato, esplora il panorama delle soluzioni in modo aggressivo, proprio come gli atomi energetici nel metallo caldo. Ha un'alta probabilità di accettare mosse che sono peggiori della sua posizione attuale. Questa è la chiave: fare una mossa "cattiva" è ciò che gli permette di uscire da un minimo locale.
Il programma di raffreddamento
Man mano che l'algoritmo viene eseguito, la temperatura viene gradualmente abbassata secondo un programma di raffreddamento. Man mano che la temperatura diminuisce, l'algoritmo diventa sempre meno propenso ad accettare una soluzione peggiore.
Alla fine, a una temperatura molto bassa, l'algoritmo si comporta come il semplice metodo di hill-climbing, accettando solo miglioramenti e affinando la sua posizione in quello che si spera sia il minimo globale.
Comprendere i compromessi
Come ogni strumento potente, la ricottura simulata non è una soluzione universale. Comprendere i suoi limiti è fondamentale per usarla efficacemente.
Punto di forza: sfuggire ai minimi locali
Il suo vantaggio principale è la capacità di navigare in paesaggi complessi e non convessi con molti minimi locali. Per problemi in cui gli algoritmi greedy falliscono costantemente, la ricottura simulata è una scelta eccellente.
Debolezza: la regolazione dei parametri è fondamentale
Le prestazioni dell'algoritmo sono altamente sensibili al programma di raffreddamento. Se raffreddato troppo rapidamente, può comunque rimanere intrappolato in un minimo locale ("quenching"). Se raffreddato troppo lentamente, può richiedere un tempo impraticabile per trovare una soluzione. Trovare il programma giusto spesso richiede sperimentazione.
Limitazione: è un metodo probabilistico
La ricottura simulata non garantisce che troverà la soluzione migliore in assoluto (il minimo globale). È un'euristica, il che significa che è progettata per trovare una soluzione molto buona in un tempo ragionevole. C'è sempre una probabilità statistica che si stabilizzi in uno stato subottimale.
Fare la scelta giusta per il tuo problema
Usa questa guida per decidere se la ricottura simulata è l'approccio corretto per il tuo compito di ottimizzazione.
- Se il tuo obiettivo principale è risolvere un problema complesso con molte trappole (minimi locali): La ricottura simulata è uno dei migliori strumenti per il lavoro, specialmente per problemi classici come il problema del commesso viaggiatore o il layout di circuiti stampati.
- Se il tuo obiettivo principale è trovare una soluzione provabilmente ottimale con la massima velocità: Dovresti prima verificare se il tuo problema è abbastanza semplice (ad esempio, convesso) da essere risolto da un algoritmo più veloce e deterministico come la programmazione lineare o un approccio greedy standard.
In definitiva, la ricottura simulata fornisce un robusto framework per navigare in spazi di ricerca vasti e difficili per trovare soluzioni di alta qualità dove i metodi più semplici falliscono.
Tabella riassuntiva:
| Caratteristica | Descrizione |
|---|---|
| Ispirazione | Processo di ricottura metallurgica (riscaldamento e raffreddamento lento) |
| Punto di forza principale | Sfuggire ai minimi locali per trovare un ottimo globale |
| Parametro chiave | Temperatura e programma di raffreddamento |
| Ideale per | Problemi di ottimizzazione complessi con molte trappole locali |
| Limitazione | Probabilistico; richiede un'attenta regolazione dei parametri |
Ottimizza la tua ricerca e sviluppo con KINTEK
Stai affrontando complessi problemi di ottimizzazione nella scienza dei materiali, nell'ingegneria chimica o nell'analisi dei dati? I principi della ricottura simulata sono ispirati a processi termici del mondo reale, e avere un controllo preciso su tali processi nel tuo laboratorio è cruciale.
KINTEK è specializzata in apparecchiature da laboratorio di alta qualità, inclusi forni e stufe avanzati che forniscono il riscaldamento uniforme e il raffreddamento controllato essenziali per la ricerca e lo sviluppo. Che tu stia sviluppando nuovi materiali o conducendo esperimenti computazionali, un'attrezzatura affidabile è la base per risultati accurati.
Contatta i nostri esperti oggi per trovare la soluzione di laboratorio perfetta per migliorare i tuoi flussi di lavoro di ottimizzazione e ottenere risultati rivoluzionari.
Guida Visiva
Prodotti correlati
Domande frequenti
- Cos'è un setacciatore vibrante? Ottieni un'analisi granulometrica accurata e ripetibile
- Quali sono i diversi tipi di agitatori per setacci? Abbina l'agitatore al tuo materiale per un'analisi accurata delle particelle
- Qual è la frequenza di un vagliatore? La chiave per un'analisi accurata della granulometria
- Qual è l'uso del setaccio vibrante (sieve shaker)? Ottieni un'analisi precisa della granulometria per il tuo laboratorio
- Cos'è un miscelatore da laboratorio? Una guida per ottenere una perfetta omogeneità del campione
